Belowground regulation of
aboveground dynamics
Gaurav Kandlikar
Louisiana State University, Baton Rouge
Life Sciences Annex A363
slides: https://talks.gklab.org/lsuplantpath-25
Sal (Shorea) dominated forests in northern India, Photo by Dhritiman Mukherjee
Intercropping of soybean and wheat; image from U. Iowa
“Christmas tree scientists work to manage grinchy fungal foes”; image from Washington State Univ
As an ecologist, my research is motivated by two overarching goals:
Explain patterns of diversity in nature
Predict responses to perturbations
Approach


Approach



Today’s talk
- Advancing ecological theory and experiments to quantify microbial effects on plant coexistence
- Microbial effects on plant communities in variable environments: Ongoing work and new directions at LSU
Photo: Tejon Ranch in southern California
Microbes play a wide variety of roles –
how to build towards generality?
Mathematical underpinning of plant–soil feedback
See also Bever, Westover, and Antonovics (1997) and Kandlikar (2024)
Plant dynamics
\[\frac{dN_1}{dt} = w_1N_1 ~~~~ \text{and} ~~~ \frac{dN_2}{dt} = w_2N_2\]
\[w_i = m_{iA}f_A + m_{iB}(1-f_A)\]
where \(f_i\) is the relative frequency of microbial community \(i\) in the soil (e.g. \(f_A = \frac{N_A}{N_A+N_B}\))
Interpretation: Plants have exponential population growth at a rate determined by the composition of the soil community.
Microbe dynamics
\[\frac{dN_A}{dt} = N_A\frac{N_1}{N_1 + N_2}~~~\text{and}~~~\frac{dN_B}{dt} = \nu N_B\frac{N_2}{N_1 + N_2}\]
Interpretation: Soil communities grow at a rate determined by the frequency of each plant (and the relative strength of each plant’s conditioning effect, \(\nu\)).
R code to simulate model dynamics
Code
psf_model <- function(time, init, params) {
with (as.list(c(time, init, params)), {
# description of parameters (see Bever et al. 1997)
# N1 and N2: abundance of the plant species 1 and 2
# p1: frequency of plant species 1; p2 = 1-pA
# m1A, m1B, m2A, m2B: conspecific and heterospecific effects of microbial community A or B on the growth of plant 1 or 2
# pA: frequency of the soil microbial community A
# v: influence of plant species 2 on the microbial community relative to that of plant 1
# Differential equations
dN1 <- (m1A*pA + m1B*(1-pA))*N1
dN2 <- (m2A*pA + m2B*(1-pA))*N2
dp1 <- p1*(1-p1)*((m1A-m2A)*pA + (m1B-m2B)*(1-pA))
dpA <- pA*(1-pA)*(p1-v*(1-p1))
# Return dN1 and dN2
return(list(c(dN1, dN2, dp1, dpA)))
})
}\[ \overbrace{(m_{1B} + m_{2A})}^{\text{interspecific effects}}- \overbrace{(m_{1A} + m_{2B})}^{\text{intraspecific effects}} > 0 \]
\[ \underbrace{\frac{1}{2}\big[\overbrace{(m_{1B} + m_{2A})}^{\text{interspecific effects}}- \overbrace{(m_{1A} + m_{2B})}^{\text{intraspecific effects}}\big]}_{\text{Stablization}} > 0 \]
Lasting influence of the Bever model
Code
# Dataset downloaded from Figshare:
# curl::curl_download("https://figshare.com/ndownloader/files/14874749", destfile = "../crawford-supplement.xlsx")
read_excel("../data/crawford-supplement.xlsx", sheet = "Data") |>
mutate(stab = -0.5*rrIs) |> # show in terms of stabilization instead of I_s
filter(stab > -3) |> # Remove the pair with Stab approx. 6 -- according to McCarthy Neuman (original author), this is likely due to bad seed survival
ggplot(aes(x = stab)) +
geom_histogram(color = "black") +
geom_histogram(fill = "#56A0D3") +
geom_rug(color = "grey25") +
geom_vline(xintercept = 0) +
annotate("text", x = Inf, y = Inf, label = "N = 1037 pairwise comparisons\n
57% experience positive stabilization",
vjust=1, hjust = 1, size = 6) +
xlab("Stabilization") + ylab("Count")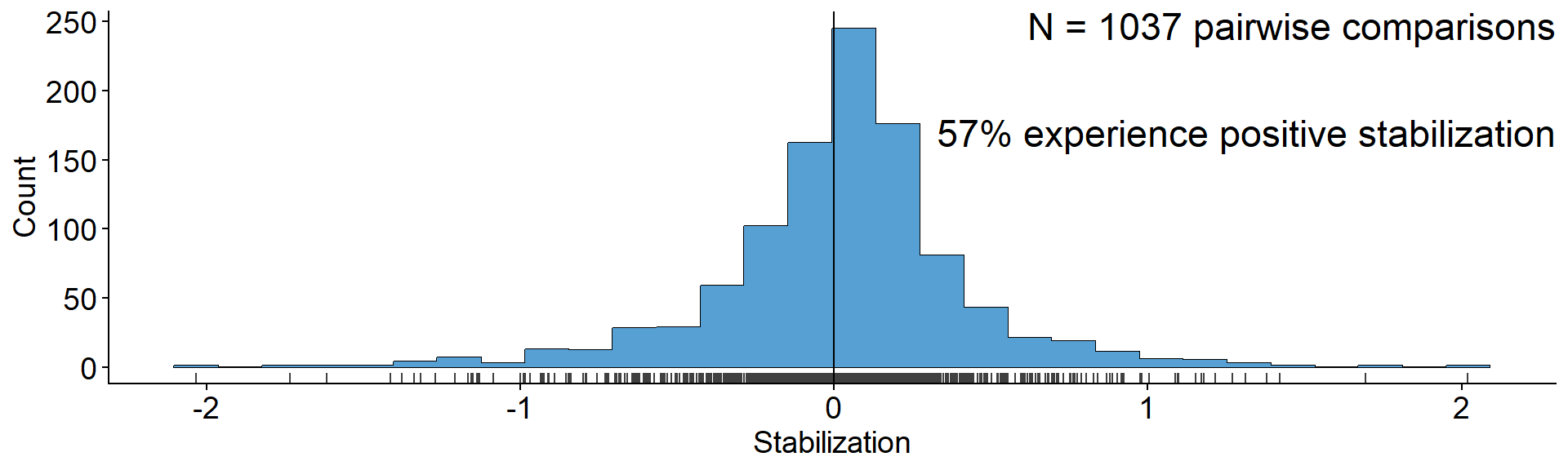
Data from Crawford et al. (2019)
A puzzle: same stabilization, different model dynamics
Code
# Define a function used for making the PSF framework
# schematic, given a set of parameter values
make_params_plot <- function(params, scale = 1.5) {
color_func <- function(x) {
ifelse(x < 0, "#EE6677", "#4477AA")
}
df <- data.frame(x = c(0,0,1,1),
y = c(0,1,0,1),
type = c("M", "P", "M", "P"))
params_plot <-
ggplot(df) +
annotate("text", x = 0, y = 1.1, size = 3.25, label = "Plant 1", color = "black", fill = "#9970ab", fontface = "bold") +
annotate("text", x = 1, y = 1.1, size = 3.25, label = "Plant 2", color = "black", fill = "#5aae61", fontface = "bold") +
annotate("text", x = 0, y = -0.15, size = 3.25, label = "Soil\nmicrobes A", label.size = 0, fill = "transparent") +
annotate("text", x = 1, y = -0.15, size = 3.25, label = "Soil\nmicrobes B", label.size = 0, fill = "transparent") +
annotate("text", x = 0.45, y = -0.4, size = 3.5, fill = "transparent",
label.size = 0.05,
label = (paste0("Stabilization = ",
0.5*(params["m1B"] + params["m2A"] - params["m1A"] - params["m2B"])))) +
geom_segment(aes(x = 0, xend = 0, y = 0.1, yend = 0.9),
arrow = arrow(length = unit(0.03, "npc")),
linewidth = abs(params["m1A"])*scale,
color = alpha(color_func(params["m1A"]), 1)) +
geom_segment(aes(x = 0.05, xend = 0.95, y = 0.1, yend = 0.9),
arrow = arrow(length = unit(0.03, "npc")),
linewidth = abs(params["m2A"])*scale,
color = alpha(color_func(params["m1B"]),1)) +
geom_segment(aes(x = 0.95, xend = 0.05, y = 0.1, yend = 0.9),
arrow = arrow(length = unit(0.03, "npc")),
linewidth = abs(params["m1B"])*scale,
color = alpha(color_func(params["m2A"]), 1)) +
geom_segment(aes(x = 1, xend = 1, y = 0.1, yend = 0.9),
arrow = arrow(length = unit(0.03, "npc"),),
linewidth = abs(params["m2B"])*scale,
color = alpha(color_func(params["m2B"]), 1)) +
# Plant cultivation of microbes
geom_segment(aes(x = -0.25, xend = -0.25, y = 0.9, yend = 0.1), linewidth = 0.15, linetype = 1,
arrow = arrow(length = unit(0.03, "npc"))) +
geom_segment(aes(x = 1.25, xend = 1.25, y = 0.9, yend = 0.1), linewidth = 0.15, linetype = 1,
arrow = arrow(length = unit(0.03, "npc"))) +
annotate("text", x = 0, y = 0.5,
label = (paste0("m1A = ", params["m1A"])),
angle = 90, vjust = -0.25, size = 3) +
annotate("text", x = 1.15, y = 0.5,
label = (paste0("m2B = ", params["m2B"])),
angle = -90, vjust = 1.5, size = 3) +
annotate("text", x = 0.75, y = 0.75,
label = (paste0("m2A = ", params["m2A"])),
angle = 45, vjust = -0.25, size = 3) +
annotate("text", x = 0.25, y = 0.75,
label = (paste0("m1B = ", params["m1B"])),
angle = -45, vjust = -0.25, size = 3) +
xlim(c(-0.4, 1.4)) +
coord_cartesian(ylim = c(-0.25, 1.15), clip = "off") +
theme_void() +
theme(legend.position = "none",
plot.caption = element_text(hjust = 0.5, size = 10))
return(params_plot)
}
# Define a function for simulating the dynamics of the
# PSF model with deSolve
params_coex <- c(m10 = 0.16, m20 = 0.16,
m1A = 0.11, m1B = 0.26,
m2A = 0.27, m2B = 0.13, v = 1)
time <- seq(0,50,0.1)
init_pA_05 <- c(N1 = 3, N2 = 7, p1 = 0.3, pA = 0.3)
out_pA_05 <- ode(y = init_pA_05, times = time, func = psf_model, parms = params_coex) |> data.frame()
params_to_plot_coex <- c(m1A = unname(params_coex["m1A"]-params_coex["m10"]),
m1B = unname(params_coex["m1B"]-params_coex["m10"]),
m2A = unname(params_coex["m2A"]-params_coex["m20"]),
m2B = unname(params_coex["m2B"]-params_coex["m20"]), v=1)
param_plot_coex <-
make_params_plot(params_to_plot_coex, scale = 6) +
annotate("text", x = 1.375, y = 0.5,
label = paste0("v = ", params_coex["v"]),
angle = -90, vjust = 1.5, size = 3)
panel_abund_coex <-
out_pA_05 |>
as_tibble() |>
select(time, N1, N2) |>
pivot_longer(N1:N2) |>
ggplot(aes(x = time, y = value, color = name)) +
geom_line(linewidth = 0.9) +
scale_color_manual(values = c("#9970ab", "#5aae61"),
name = "Plant species", label = c("Plant 1", "Plant 2"), guide = "none") +
scale_y_continuous(breaks = c(2e4, 4e4, 6e4, 8e4), labels = scales::scientific) +
ylab("Abundance") +
theme(axis.title = element_text(size = 10))
# Panel D: plot for frequencies of both plants when growing
# in dynamic soils
panel_freq_coex <-
out_pA_05 |>
as_tibble() |>
mutate(p2 = 1-p1) |>
select(time, p1, p2) |>
pivot_longer(p1:p2) |>
ggplot(aes(x = time, y = value, color = name)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = c("#9970ab", "#5aae61"),
name = "Plant species", label = c("Plant 1", "Plant 2")) +
scale_y_continuous(limits = c(0,1), breaks = c(0, 0.5, 1)) +
ylab("Frequency") +
theme(axis.title = element_text(size = 10))
param_plot_coex + {panel_abund_coex+panel_freq_coex &
theme(axis.text = element_text(size = 8), legend.position = 'none')} +
plot_layout(widths = c(1/3, 2/3))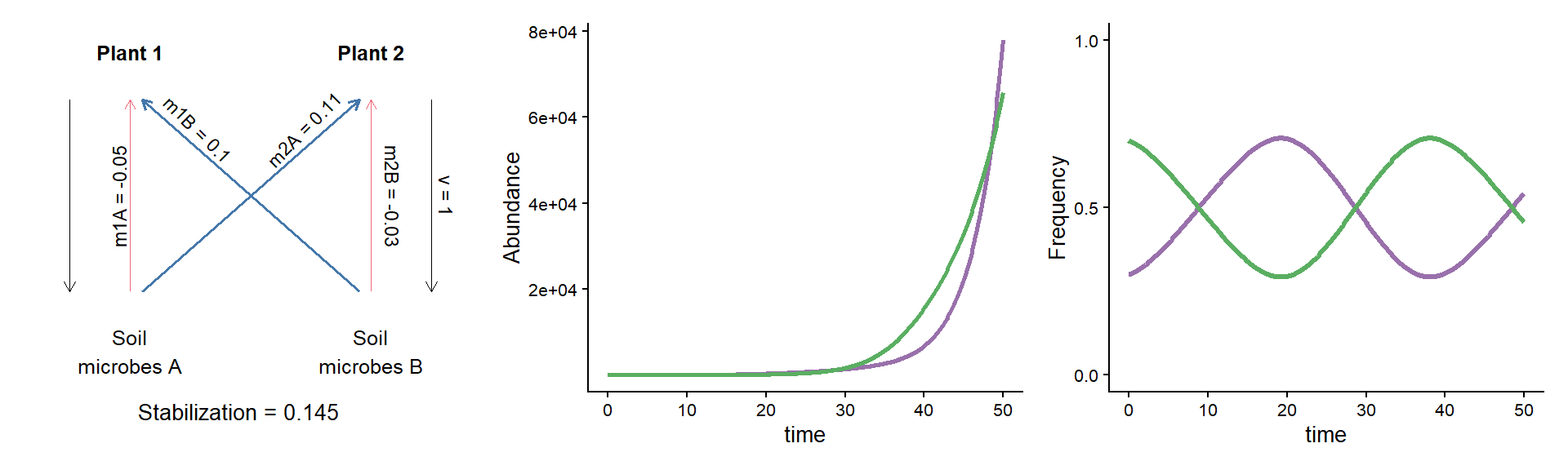
Code
# Define a function for simulating the dynamics of the
# PSF model with deSolve
params <- c(m10 = 0.16, m20 = 0.16,
m1A = 0.02, m2A = 0.33,
m1B = 0.18, m2B = 0.20, v = 1)
time <- seq(0,200,0.1)
init_pA_05 <- c(N1 = 3, N2 = 7, p1 = 0.3, pA = 0.3)
out_pA_05 <- ode(y = init_pA_05, times = time, func = psf_model, parms = params) |> data.frame()
params_to_plot <- c(m1A = unname(params["m1A"]-params["m10"]),
m1B = unname(params["m1B"]-params["m10"]),
m2A = unname(params["m2A"]-params["m20"]),
m2B = unname(params["m2B"]-params["m20"]), v=1)
param_plot <-
make_params_plot(params_to_plot, scale = 6) +
annotate("text", x = 1.375, y = 0.5,
label = paste0("v = ", params["v"]),
angle = -90, vjust = 1.5, size = 3)
panel_abund <-
out_pA_05 |>
as_tibble() |>
select(time, N1, N2) |>
pivot_longer(N1:N2) |>
ggplot(aes(x = time, y = value, color = name)) +
geom_line(linewidth = 0.9) +
scale_color_manual(values = c("#9970ab", "#5aae61"),
name = "Plant species", label = c("Plant 1", "Plant 2"), guide = "none") +
scale_y_continuous(breaks = c(0,8e17,1.6e18), labels = c("0", "7e17","1.4e18")) +
ylab("Abundance")
# Panel D: plot for frequencies of both plants when growing
# in dynamic soils
panel_freq <-
out_pA_05 |>
as_tibble() |>
mutate(p2 = 1-p1) |>
select(time, p1, p2) |>
pivot_longer(p1:p2) |>
ggplot(aes(x = time, y = value, color = name)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = c("#9970ab", "#5aae61"),
name = "Plant species", label = c("Plant 1", "Plant 2")) +
scale_y_continuous(limits = c(0,1), breaks = c(0, 0.5, 1)) +
ylab("Frequency")
param_plot + {panel_abund + panel_freq &
theme(axis.text = element_text(size = 8), legend.position = 'none')} +
plot_layout(widths = c(1/3, 2/3))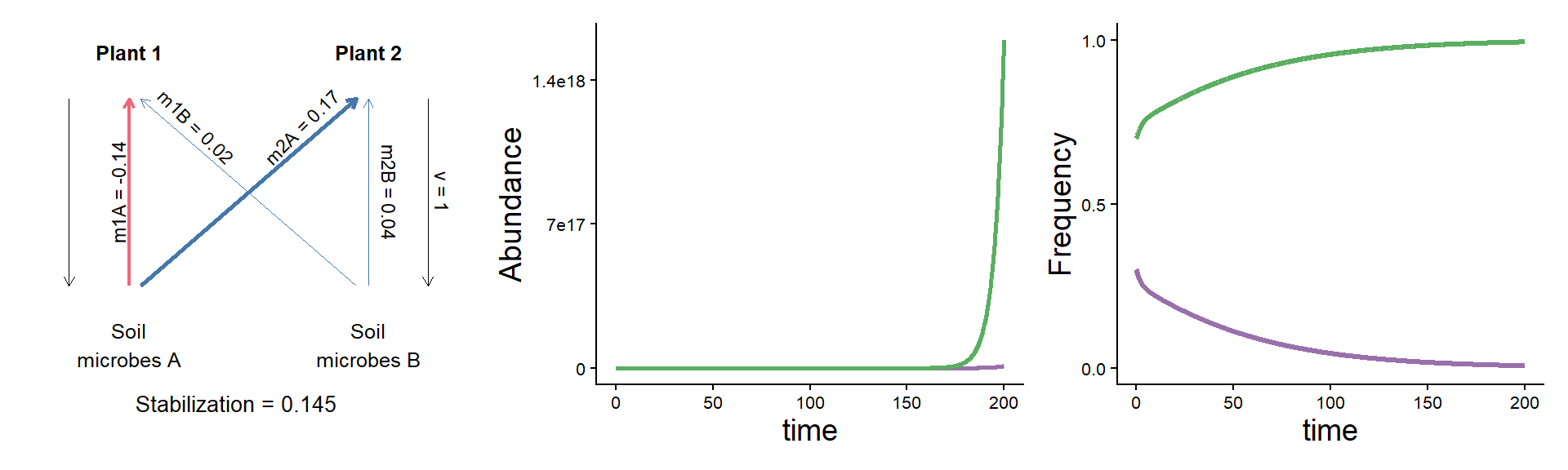
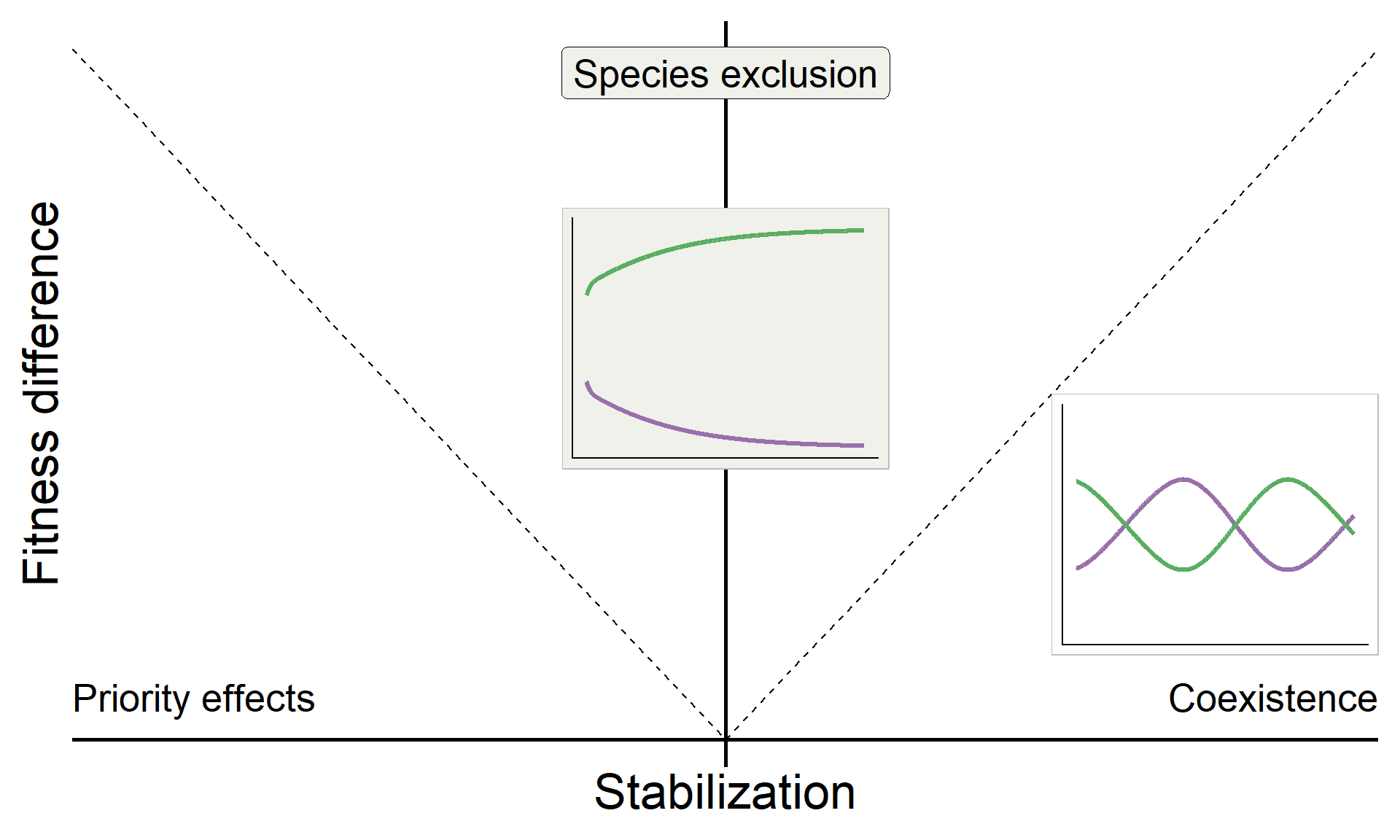
How can we more accurately infer predicted plant dynamics under plant–soil feedback?
Build on insights from coexistence theory (Chesson 2018):
- Stablization is necessary for coexistence but doesn’t guarantee coexistence
- Stable coexistence is possible only when stabilization overcomes competitive imbalances (fitness differences)

How can we more accurately infer predicted plant dynamics under plant–soil feedback?
How can we more accurately infer predicted plant dynamics under plant–soil feedback?

How can we more accurately infer predicted plant dynamics under plant–soil feedback?

How can we more accurately infer predicted plant dynamics under plant–soil feedback?

\[\text{Fitness difference}_{1,2} = \overbrace{\frac{1}{2}(m_{1A}+m_{1B})}^{\substack{\text{Sensitivity of}\\ \text{Sp 1 to microbes}}} - \overbrace{\frac{1}{2}(m_{2A}+m_{2B})}^{\substack{\text{Sensitivity of}\\ \text{Sp 2 to microbes}}}\]
Code
base <-
tibble(sd = seq(-1,1,0.1),
fd = c(seq(1,0,-0.1), seq(0.1,1,0.1))) |>
ggplot(aes(x = sd, y = fd)) +
geom_line(linetype = "dashed") +
geom_hline(yintercept = 0, linewidth = 1) +
geom_vline(xintercept = 0, linewidth = 1) +
xlab("Stabilization") +
ylab("Fitness difference") +
theme(axis.text = element_blank(),
axis.ticks = element_blank(),
axis.line = element_blank(),
axis.title = element_text(size = 25)) +
scale_x_continuous(expand = c(0,0)) +
scale_y_continuous(expand = c(0.04,0))
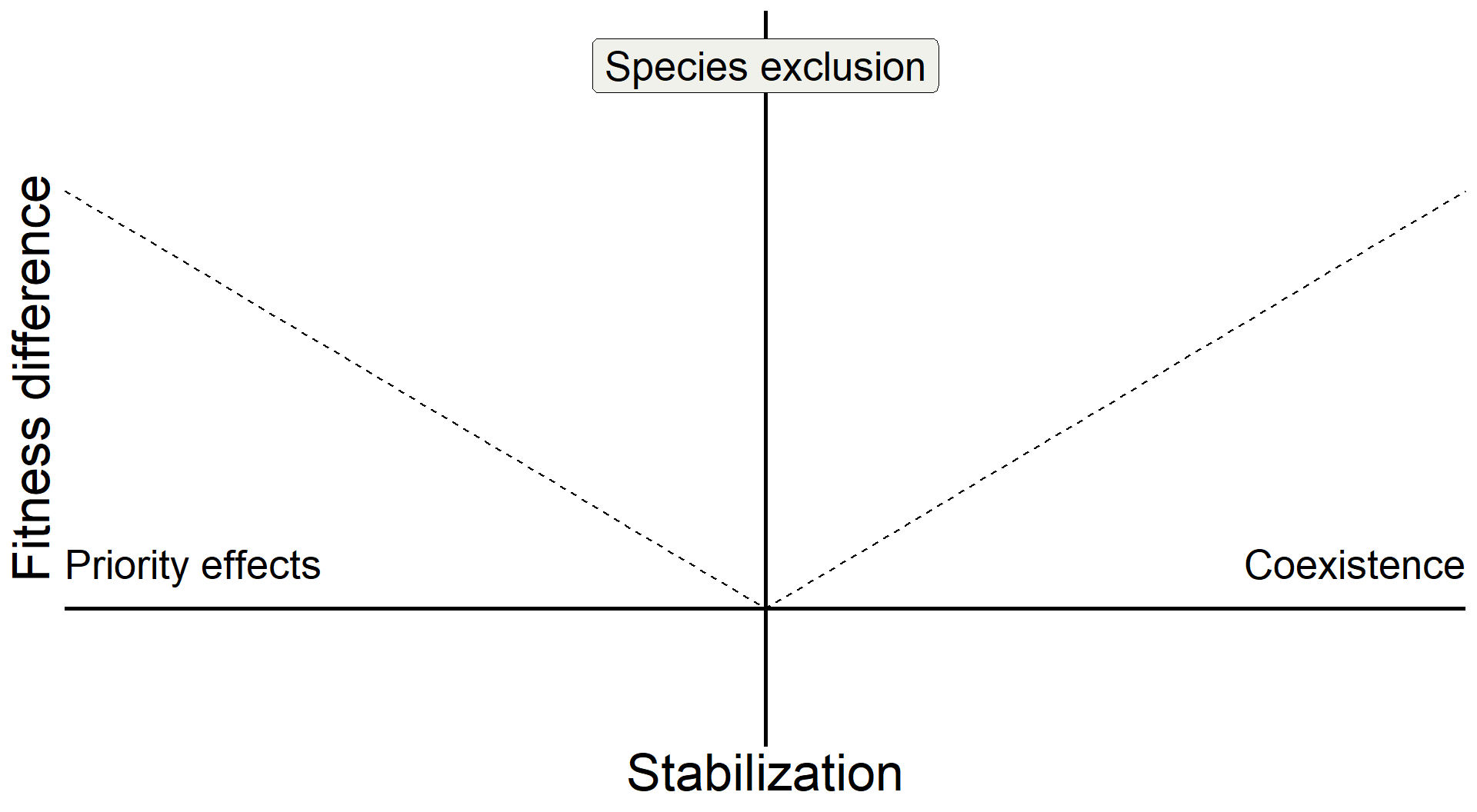
base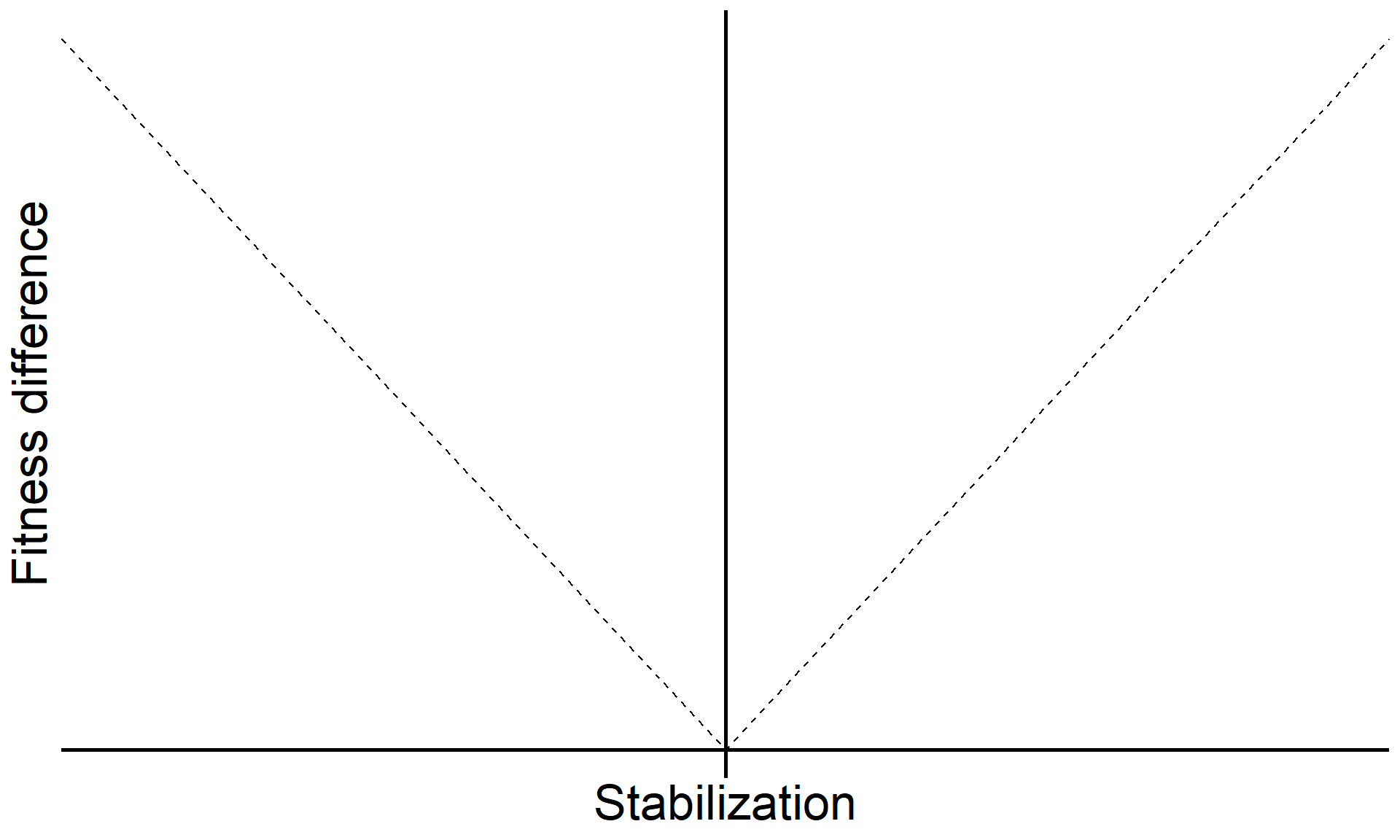
Code
base <-
base +
annotate("text", x = Inf, y = 0, hjust = 1, vjust = -1, label = "Coexistence", size = 7, family = "italic") +
annotate("text", x = -Inf, y = 0, hjust = 0, vjust = -1, label = "Priority effects", size = 7, family = "italic") +
annotate("label", x = 0, y = Inf, vjust = 1.5, label = "Species exclusion", size = 7, fill = "#F0F1EB",family = "italic")
base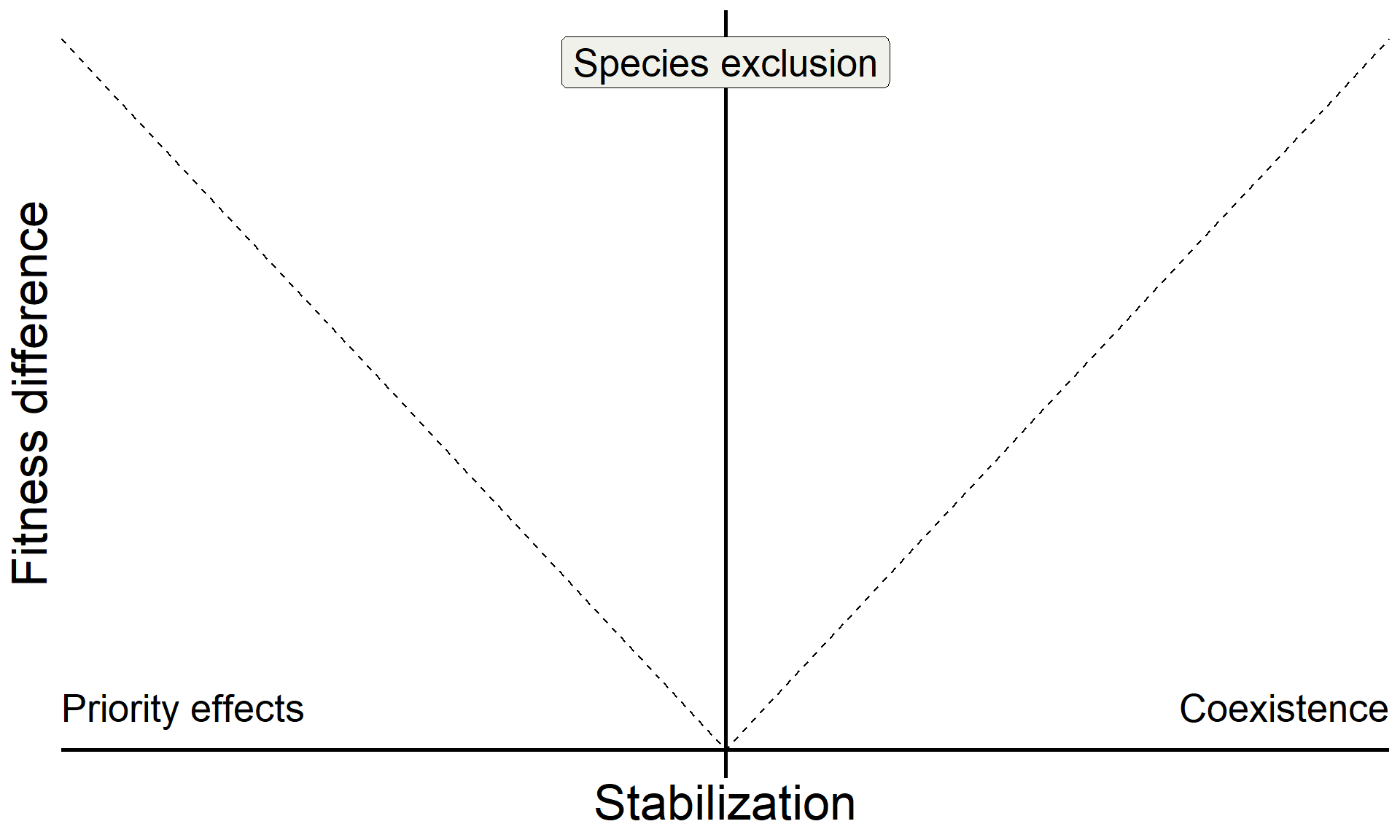
Code
metrics <- function(params) {
IS <- with(as.list(params), {m1A - m2A - m1B + m2B})
FD <- with(as.list(params), {(1/2)*(m1A+m2A) - (1/2)*(m1B+m2B)})
SD <- (-1/2)*IS
return(c(IS = IS, SD = SD, FD = FD))
}
coex_metrics <- metrics(params_coex)
base_coex <-
base +
inset_element({panel_freq_coex + theme(legend.position = 'none',
axis.text = element_blank(),
axis.ticks = element_blank(),
axis.title = element_blank(),
plot.background = element_rect(color = "grey"))},
0.75,0.15,1,0.5)
base_coex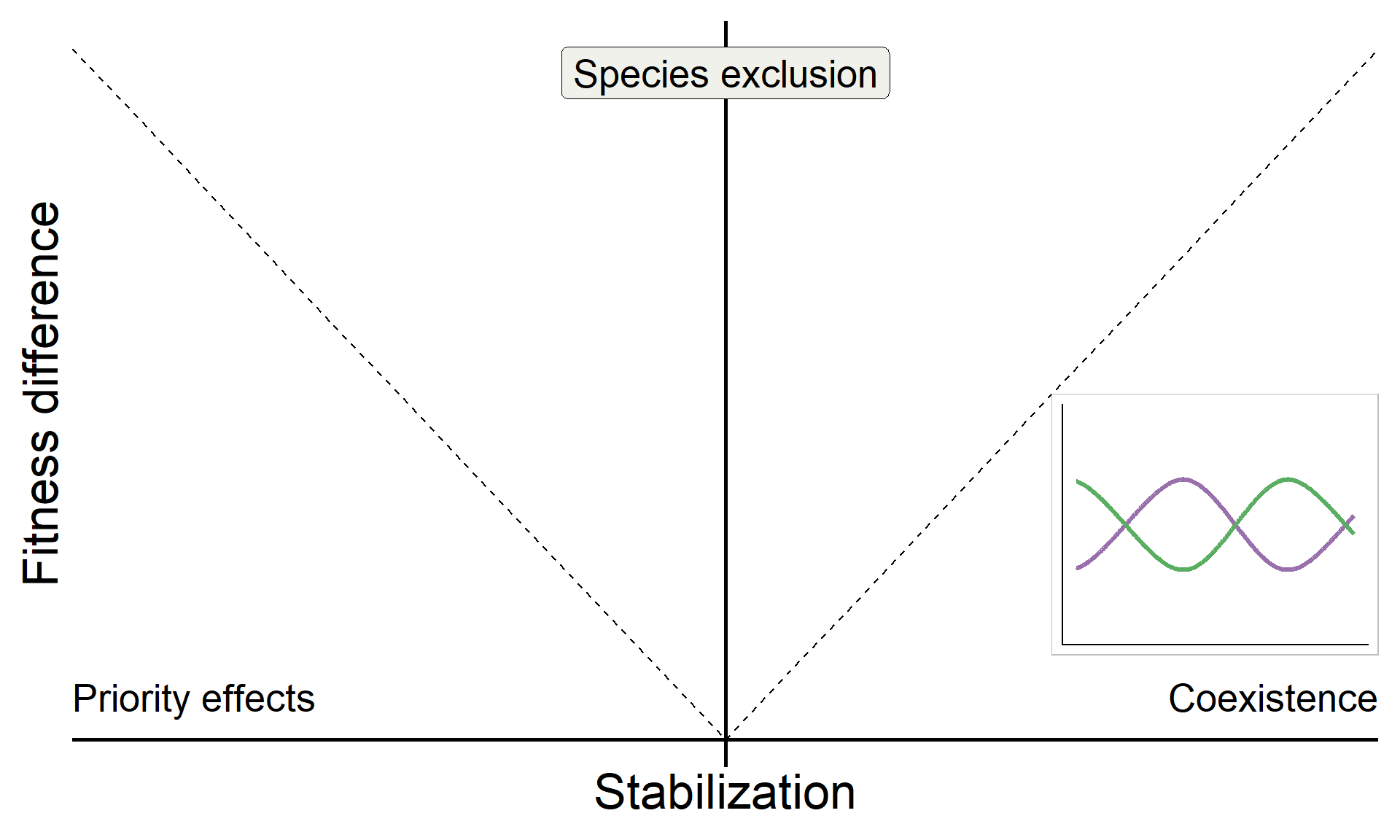
Do microbes generate fitness differences in nature?
Sedgwick Reserve (unceded territory of Chumash people)

Code
# Example point, using UR_FE values
base +
annotate("pointrange", x = 0.275, y = 0.0591, ymin = 0.0591-0.307,ymax = 0.0591+0.307, shape = 21, stroke = 1.5, size = 1, linewidth = 0.1, fill = "#4477aa") +
annotate("pointrange", x = 0.275, y = 0.0591, xmin = 0.275-0.152,xmax = 0.275+0.152, shape = 21, fill = "#4477aa", linewidth = 0.1, size = 1, stroke = 1.5) +
annotate("text", x = 0.275 + 0.3, y = 0.0591 + 0.15, color = "#4477aa", label = "Festuca - Plantago", size = 8, fontface = "italic") +
theme(axis.title = element_blank())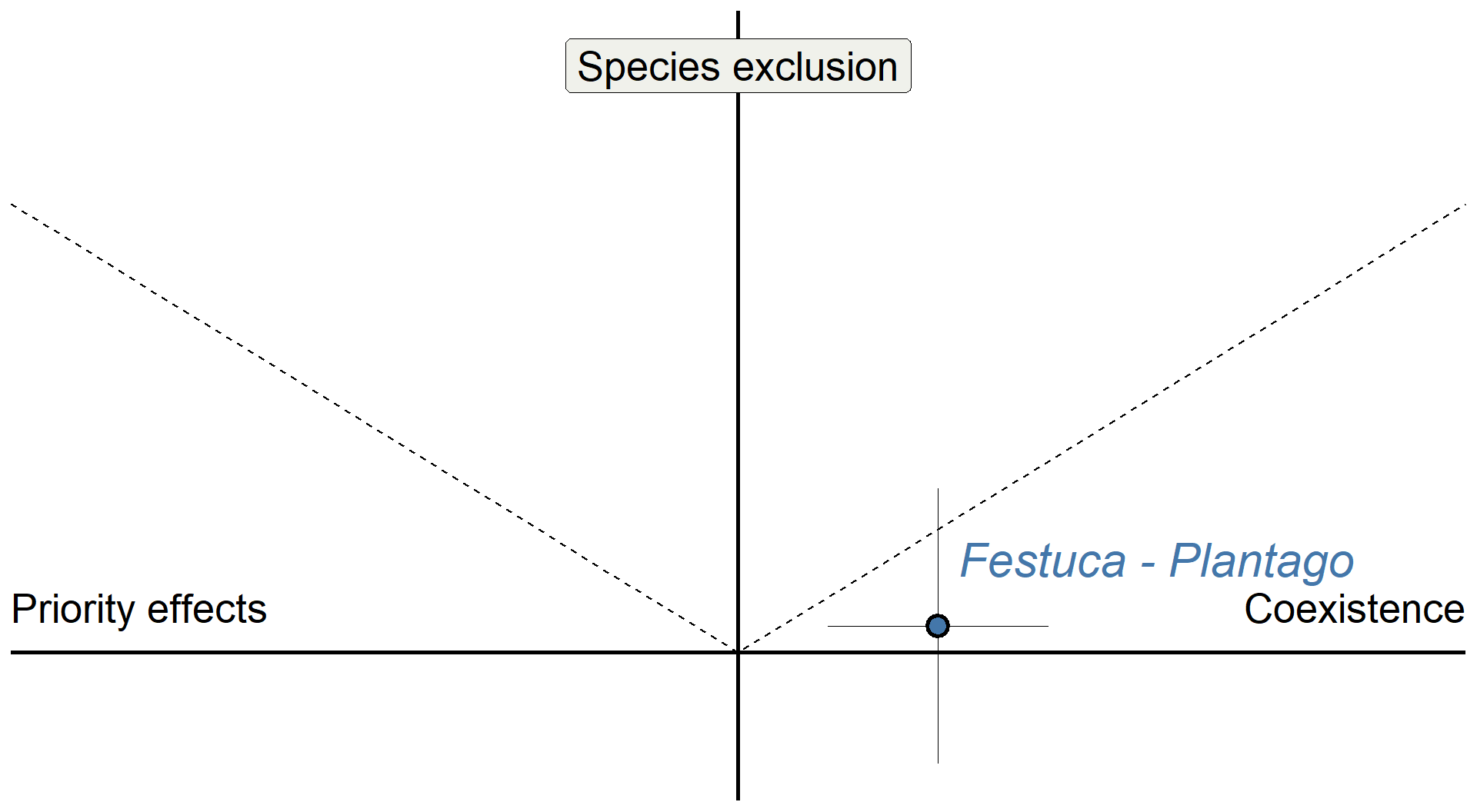
Code
# Dataset downloaded from Figshare:
# curl::curl_download("https://datadryad.org/downloads/file_stream/367188", destfile = "../data/kandlikar2021-supplement.csv")
biomass_wide <-
read_csv("../data/kandlikar2021-supplement.csv") |>
mutate(log_agb = log(abg_dry_g)) |>
mutate(source_soil = ifelse(source_soil == "aastr", "str", source_soil),
source_soil = ifelse(source_soil == "abfld", "fld", source_soil),
pair = paste0(source_soil, "_", focal_species)) |>
select(replicate, pair, log_agb) |>
pivot_wider(names_from = pair, values_from = log_agb) |>
filter(!is.na(replicate))
# Calculate the Stabilization between each species pair ----
# Recall that following the definition of the m terms in Bever 1997,
# and the analysis of this model in Kandlikar 2019,
# stablization = -0.5*(log(m1A) + log(m2B) - log(m1B) - log(m2A))
# Here is a function that does this calculation
# (recall that after the data reshaping above,
# each column represents a given value of log(m1A))
calculate_stabilization <- function(df) {
df |>
# In df, each row is one repilcate/rack, and each column
# represents the growth of one species in one soil type.
# e.g. "FE_ACWR" is the growth of FE in ACWR-cultivated soil.
mutate(AC_FE = -0.5*(AC_ACWR - AC_FEMI - FE_ACWR + FE_FEMI),
AC_HO = -0.5*(AC_ACWR - AC_HOMU - HO_ACWR + HO_HOMU),
AC_SA = -0.5*(AC_ACWR - AC_SACO - SA_ACWR + SA_SACO),
AC_PL = -0.5*(AC_ACWR - AC_PLER - PL_ACWR + PL_PLER),
AC_UR = -0.5*(AC_ACWR - AC_URLI - UR_ACWR + UR_URLI),
FE_HO = -0.5*(FE_FEMI - FE_HOMU - HO_FEMI + HO_HOMU),
FE_SA = -0.5*(FE_FEMI - FE_SACO - SA_FEMI + SA_SACO),
FE_PL = -0.5*(FE_FEMI - FE_PLER - PL_FEMI + PL_PLER),
FE_UR = -0.5*(FE_FEMI - FE_URLI - UR_FEMI + UR_URLI),
HO_PL = -0.5*(HO_HOMU - HO_PLER - PL_HOMU + PL_PLER),
HO_SA = -0.5*(HO_HOMU - HO_SACO - SA_HOMU + SA_SACO),
HO_UR = -0.5*(HO_HOMU - HO_URLI - UR_HOMU + UR_URLI),
SA_PL = -0.5*(SA_SACO - SA_PLER - PL_SACO + PL_PLER),
SA_UR = -0.5*(SA_SACO - SA_URLI - UR_SACO + UR_URLI),
PL_UR = -0.5*(PL_PLER - PL_URLI - UR_PLER + UR_URLI)) |>
select(replicate, AC_FE:PL_UR) |>
gather(pair, stabilization, AC_FE:PL_UR)
}
stabilization_values <- calculate_stabilization(biomass_wide)
# Seven values are NA; we can omit these
stabilization_values <- stabilization_values |>
filter(!(is.na(stabilization)))
# Calculating the Fitness difference between each species pair ----
# Similarly, we can now calculate the fitness difference between
# each pair. Recall that FD = 0.5*(log(m1A)+log(m1B)-log(m2A)-log(m2B))
# But recall that here, IT IS IMPORTANT THAT
# m1A = (m1_soilA - m1_fieldSoil)!
# The following function does this calculation:
calculate_fitdiffs <- function(df) {
df |>
mutate(AC_FE = 0.5*((AC_ACWR-fld_ACWR) + (FE_ACWR-fld_ACWR) - (AC_FEMI-fld_FEMI) - (FE_FEMI-fld_FEMI)),
AC_HO = 0.5*((AC_ACWR-fld_ACWR) + (HO_ACWR-fld_ACWR) - (AC_HOMU-fld_HOMU) - (HO_HOMU-fld_HOMU)),
AC_SA = 0.5*((AC_ACWR-fld_ACWR) + (SA_ACWR-fld_ACWR) - (AC_SACO-fld_SACO) - (SA_SACO-fld_SACO)),
AC_PL = 0.5*((AC_ACWR-fld_ACWR) + (PL_ACWR-fld_ACWR) - (AC_PLER-fld_PLER) - (PL_PLER-fld_PLER)),
AC_UR = 0.5*((AC_ACWR-fld_ACWR) + (UR_ACWR-fld_ACWR) - (AC_URLI-fld_URLI) - (UR_URLI-fld_URLI)),
FE_HO = 0.5*((FE_FEMI-fld_FEMI) + (HO_FEMI-fld_FEMI) - (FE_HOMU-fld_HOMU) - (HO_HOMU-fld_HOMU)),
FE_SA = 0.5*((FE_FEMI-fld_FEMI) + (SA_FEMI-fld_FEMI) - (FE_SACO-fld_SACO) - (SA_SACO-fld_SACO)),
FE_PL = 0.5*((FE_FEMI-fld_FEMI) + (PL_FEMI-fld_FEMI) - (FE_PLER-fld_PLER) - (PL_PLER-fld_PLER)),
FE_UR = 0.5*((FE_FEMI-fld_FEMI) + (UR_FEMI-fld_FEMI) - (FE_URLI-fld_URLI) - (UR_URLI-fld_URLI)),
HO_PL = 0.5*((HO_HOMU-fld_HOMU) + (PL_HOMU-fld_HOMU) - (HO_PLER-fld_PLER) - (PL_PLER-fld_PLER)),
HO_SA = 0.5*((HO_HOMU-fld_HOMU) + (SA_HOMU-fld_HOMU) - (HO_SACO-fld_SACO) - (SA_SACO-fld_SACO)),
HO_UR = 0.5*((HO_HOMU-fld_HOMU) + (UR_HOMU-fld_HOMU) - (HO_URLI-fld_URLI) - (UR_URLI-fld_URLI)),
SA_PL = 0.5*((SA_SACO-fld_SACO) + (PL_SACO-fld_SACO) - (SA_PLER-fld_PLER) - (PL_PLER-fld_PLER)),
SA_UR = 0.5*((SA_SACO-fld_SACO) + (UR_SACO-fld_SACO) - (SA_URLI-fld_URLI) - (UR_URLI-fld_URLI)),
PL_UR = 0.5*((PL_PLER-fld_PLER) + (UR_PLER-fld_PLER) - (PL_URLI-fld_URLI) - (UR_URLI-fld_URLI))) |>
select(replicate, AC_FE:PL_UR) |>
gather(pair, fitdiff_fld, AC_FE:PL_UR)
}
fd_values <- calculate_fitdiffs(biomass_wide)
# Twenty-two values are NA; let's omit these.
fd_values <- fd_values |> filter(!(is.na(fitdiff_fld)))
# Now, generate statistical summaries of SD and FD
stabiliation_summary <- stabilization_values |> group_by(pair) |>
summarize(mean_sd = mean(stabilization),
sem_sd = sd(stabilization)/sqrt(n()),
n_sd = n())
fitdiff_summary <- fd_values |> group_by(pair) |>
summarize(mean_fd = mean(fitdiff_fld),
sem_fd = sd(fitdiff_fld)/sqrt(n()),
n_fd = n())
# Combine the two separate data frames.
sd_fd_summary <- left_join(stabiliation_summary, fitdiff_summary)
# Some of the FDs are negative, let's flip these to be positive
# and also flip the label so that the first species in the name
# is always the fitness superior.
sd_fd_summary <- sd_fd_summary |>
# if mean_fd is < 0, the following command gets the absolute
# value and also flips around the species code so that
# the fitness superior is always the first species in the code
mutate(pair = ifelse(mean_fd < 0,
paste0(str_extract(pair, "..$"),
"_",
str_extract(pair, "^..")),
pair),
mean_fd = abs(mean_fd))
sd_fd_summary <-
sd_fd_summary |>
mutate(
# outcome = ifelse(mean_fd - 2*sem_fd >
# mean_sd + 2*sem_sd, "exclusion", "neutral"),
outcome2 = ifelse(mean_fd > mean_sd, "exclusion", "coexistence"),
outcome2 = ifelse(mean_sd < 0, "exclusion or priority effect", outcome2)
)
base +
geom_pointrange(data = sd_fd_summary,
aes(x = mean_sd, y = mean_fd,
ymin = mean_fd-sem_fd,
ymax = mean_fd+sem_fd, fill = outcome2), size = 1, linewidth = 0.1,
shape = 21, stroke = 1.5) +
geom_pointrange(data = sd_fd_summary,
aes(x = mean_sd, y = mean_fd,
xmin = mean_sd-sem_sd,
xmax = mean_sd+sem_sd, fill = outcome2), size = 1, linewidth = 0.1, shape = 21, stroke = 1.5) +
scale_fill_manual(values = c("#4477aa", "#ee6677", "#ccbb44")) +
theme(legend.position = "none")+
theme(axis.title = element_blank())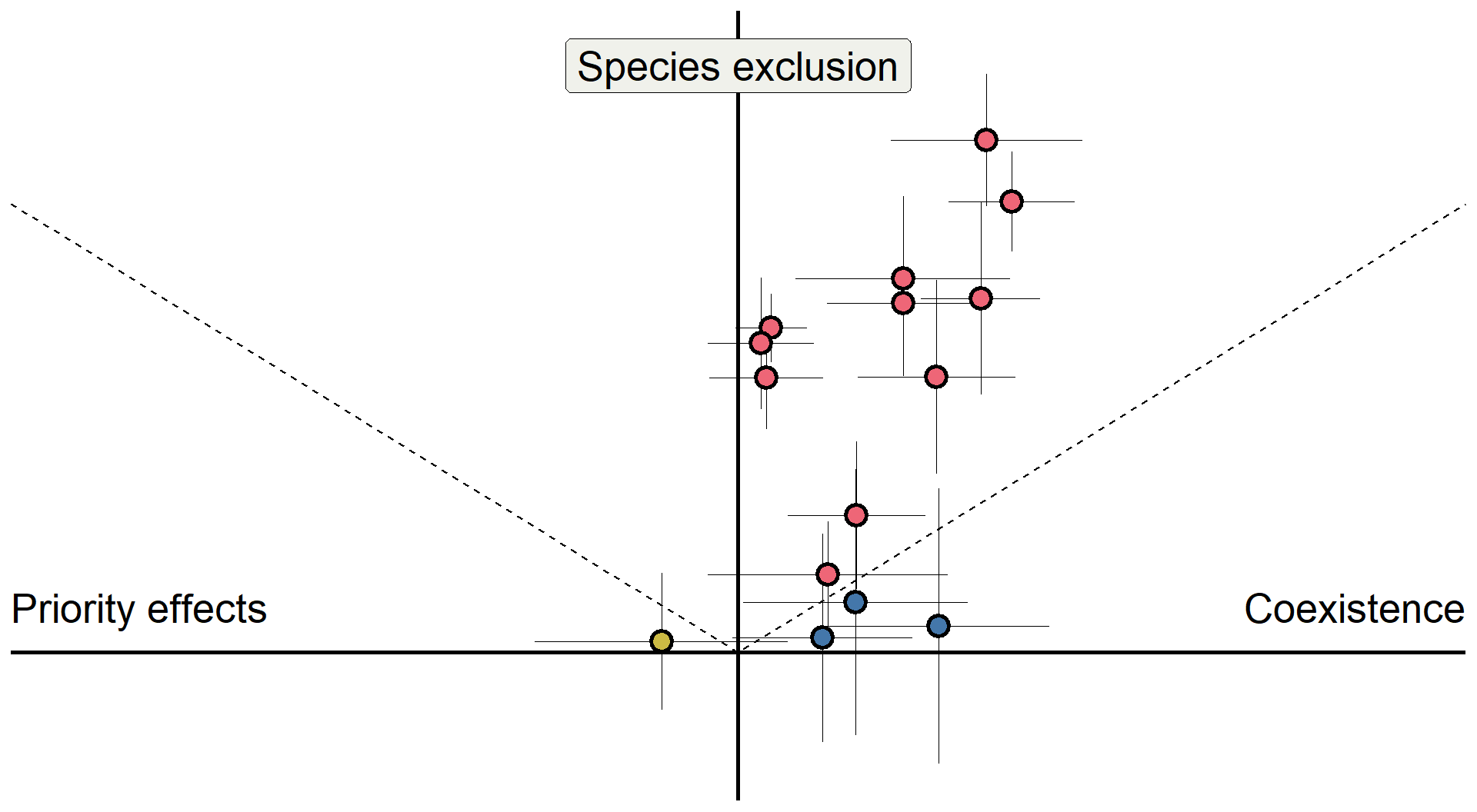
Detailed in Kandlikar et al. (2021)
Do microbes generate fitness differences in nature?
In California grasslands, microbes tend to drive stronger fitness differences than stabilization.
Can we answer this question more generally?

Meta-analysis overview
Data for 518 pairwise comparisons of stabilization and fitness differences (results shown for 72 pairs here)
New sampling approach for quantifying uncertainty in coexistence outcomes
Results in Yan, Levine, and Kandlikar (2022); Analyses available on Zenodo
Do microbes generate fitness differences in nature?
- Fitness differences represent a dominant avenue through which microbes control plant coexistence
Microbially-mediated intransitivity in pine-oak forests in Spain, Pajares-Murgó et al. (2024)
Today’s talk
- Ecological theory for microbial effects on plant coexistence
2. Microbial effects on plant communities in variable environments
Today’s talk
- Ecological theory for microbial effects on plant coexistence
2. Microbial effects on plant communities in variable environments
General theme: Advancing fundamental ecological insights in light of conservation and management challenges
Woody encroachment in longleaf pine understories
Coexistence in fragmented tropical forests
Plant eco-evolutionary dynamics under drought
Historical range of the longleaf pine ecosystem
Code
library(sf)
library(tidyverse)
little <- sf::st_read("../img/pinupalu.shp")
## Reading layer `pinupalu' from data source
## `C:\Users\gkandlikar\Desktop\gklab\talks\img\pinupalu.shp'
## using driver `ESRI Shapefile'
## Simple feature collection with 38 features and 5 fields
## Geometry type: POLYGON
## Dimension: XY
## Bounding box: xmin: -95.21806 ymin: 26.61921 xmax: -75.79999 ymax: 36.84856
## CRS: NA
# States we want to show
llp_states <- c("texas", "louisiana","mississippi", "alabama", "florida", "georgia", "south carolina", "north carolina", "virginia", "tennessee")
states <- map_data("state") |>
filter(region %in% llp_states)
ggplot() +
geom_polygon(data = states,
aes(x = long, y = lat, group = group), fill = "transparent", color = 'darkgrey') +
geom_sf(data = little, fill = alpha('#228833', 0.5)) +
theme_void()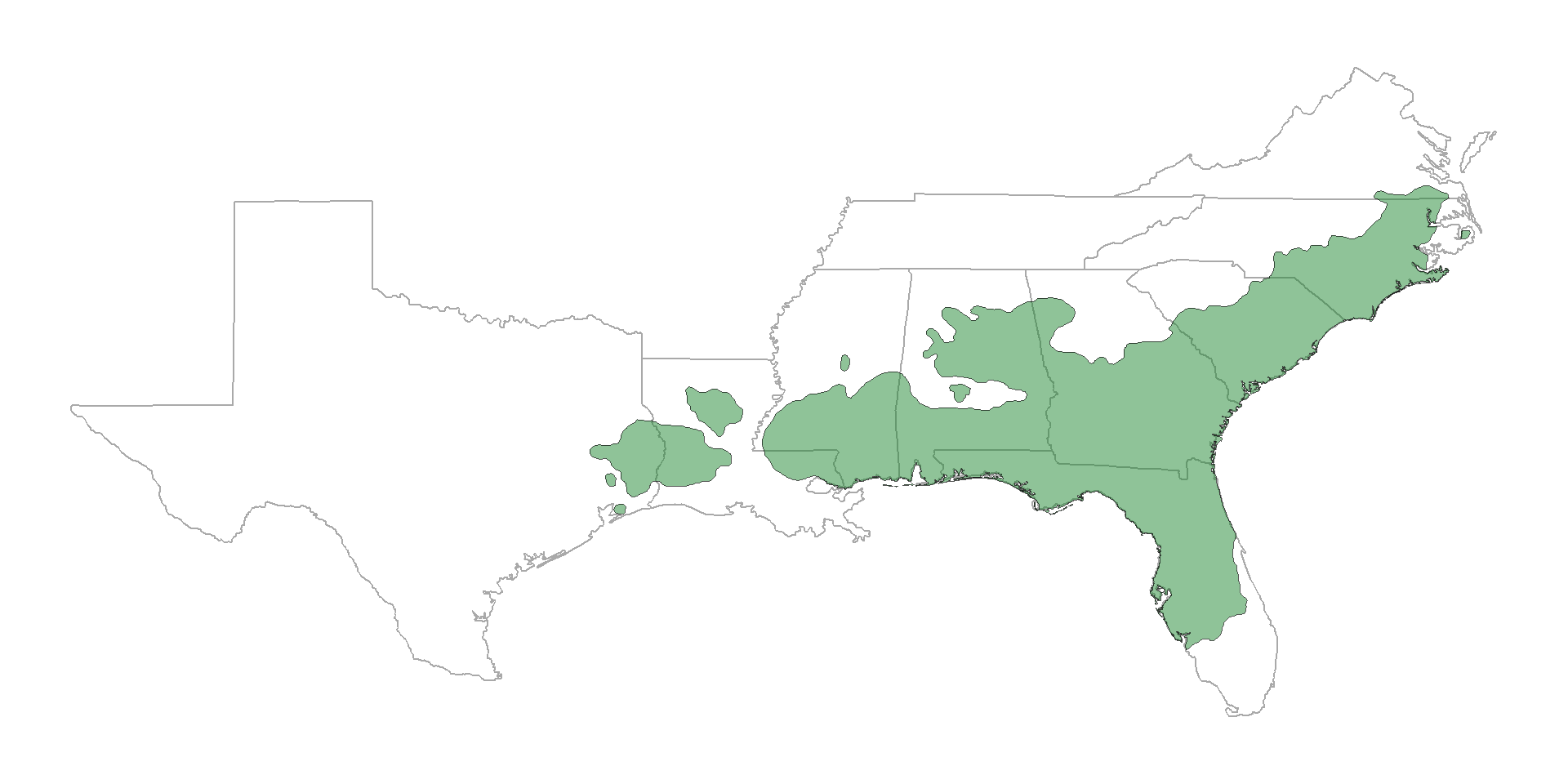
Photo: Kandlikar lab members at Lee Memorial Forest (LSU Ag Center), Franklinton LA
Fire helps maintain the open understory


Understory plant communities are among the most species–rich in North America!
Our question: Do microbes play a role in “shrubification” of unburned understories?
Across ecosystems, grasses tend to experience negative feedback
Code
# curl::curl_download("https://datadryad.org/downloads/file_stream/2789266", destfile = "../data/jiang2024-dataset.csv")
jiang_dat <- read_csv("../data/jiang2024-dataset.csv")
# jiang_metamod <- metafor::rma.mv(rr, var, data = jiang_dat, mods = ~ Life.form-1)
# saveRDS(jiang_metamod, "../data/jiang-metamod.rds")
metamod <- readRDS("../data/jiang-metamod.rds")
metamod_s <- broom::tidy(metamod)
jiang_dat |>
ggplot(aes(x = rr, y = Life.form, color = Life.form)) +
ggbeeswarm::geom_quasirandom(shape = 21) +
scale_color_manual(values = c("#ccbb44","#228833")) +
annotate("point",
x = metamod_s$estimate[1], y = 1, size = 3, shape = 21, stroke = 1.5) +
annotate("point",
x = metamod_s$estimate[2], y = 2, size = 3, shape = 21, stroke = 1.5) +
ylab("") +
xlab("Growth in self vs. growth in non-self") +
xlim(-2.5,2.5)+
geom_vline(xintercept = 0, linetype = 'dashed') +
theme(legend.position = "none",
axis.text.y = element_text(size = 12, color = 'black'))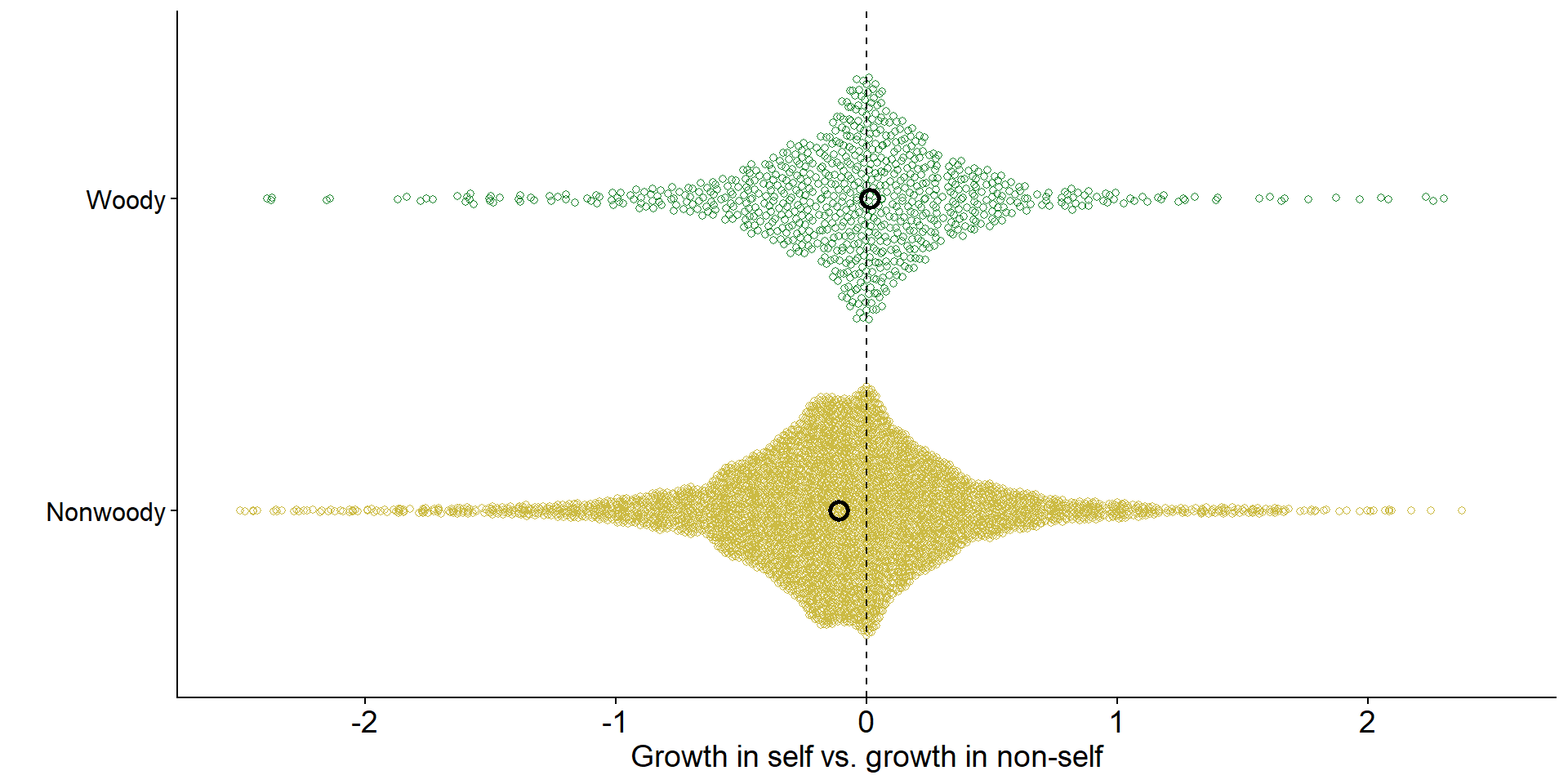
Data from Jiang et al. (2024)
Common shrubs in longleaf pine understories
(Quercus marilandica)

(Vaccinium arboreum)
Common shrubs in longleaf pine understories
(Quercus marilandica)
Associates with ectomycorrhial fungi

(Vaccinium arboreum)
Associates with ericoid mycorrhizal fungi
Most herbaceous plants here associate with arbuscular mycorrhizae
Soil feedbacks vary by mycorrhizal type
Code
# download.file("https://www.science.org/doi/suppl/10.1126/science.aai8212/suppl_file/bennett_aai8212_database-s1.xlsx", destfile = "../data/bennett2017-dataset.xlsx")
readxl::read_xlsx("../data/bennett-2017.xlsx", sheet = 2) |>
mutate(`Type of Mycorrhiza` = factor(`Type of Mycorrhiza`, c("EM", "AM"))) |>
mutate(logratio = log(`Average of Biomass in Conspecific Soil`/`Average of Biomass in Heterospecific Soil`)) |>
arrange(logratio) |>
mutate(rown = row_number()) |>
ggplot(aes(x = logratio, color = `Type of Mycorrhiza`, y = rown, shape = `Type of Mycorrhiza`)) +
geom_point(size = 2) +
geom_segment(aes(x = 0, xend = logratio), linewidth = 0.125) +
xlab("Growth in self-conditioned microbes vs.\n nonself-conditioned microbes") +
geom_vline(xintercept = 0) +
scale_color_manual(values = c("#0077bb", "#cc3311")) +
theme(axis.line.y = element_blank(),
axis.text.y = element_blank(),
axis.title.y = element_blank(),
axis.ticks.y = element_blank(),
legend.position = "inside",
legend.position.inside = c(0.9, 0.1),
legend.text = element_text(size = 12),
legend.title = element_blank())
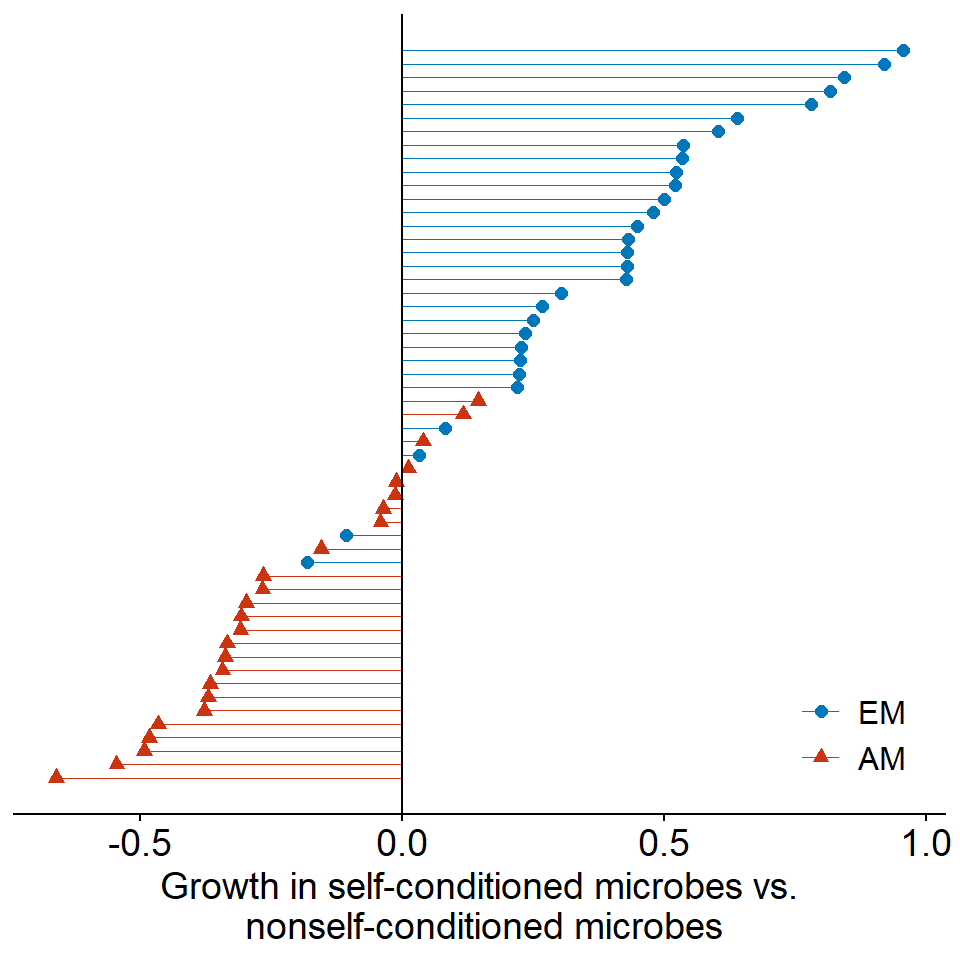
Data from Bennett et al. (2017)
Do soil microbes play a role in driving shrubification under fire suppression?
What are the direct impacts of fire on soil microbial dynamics?
Does the history and severity of fire mediate the impact of soil microbes on plant performance and coexistence?

Postdoc
Approach
Mathematical modeling: experimentally-informed dynamics of plant community dynamics (in prep)
Field observations and experiment: evaluate fire effects on soil communities (ongoing)
Hoophouse experiment: evaluate shrub and grass growth in shrub- and grass-conditioned soils with different burn histories (planned, Spring 2026)
Supported with funds from Louisiana State Board of Research RCS program
Mathematical modeling of plant dynamics
Transitions between patches
Patches without plants or soil conditioning
\[\frac{dP_{00}}{dt} = \overbrace{\mu_g P_{g0} +\mu_s P_{s0}}^{\substack{\text{ plant mortality}}\\{\text{in unconditioned soil}}} + \overbrace{d_g P_{0g} + d_s P_{0s}}^{\substack{\text{microbial decay in} \\ \text{empty-but-conditioned patches} }} - \\ \overbrace{r_gP_{00}(P_{{g0}+}P_{gg}+P_{gs})}^{\text{grass establishment}} - \\ \overbrace{r_sP_{00}(P_{{s0}+}P_{ss}+P_{sg})}^{\text{shrub establishment}} \]
Patches with plant present but soil not yet conditioned
\[\frac{dP_{g0}}{dt} = \overbrace{r_gP_{00}(P_{g0} + P_{gg} + P_{gs})}^{\substack{\text{grass establishment in} \\ \text{unconditioned soil}}} - \overbrace{c_g P_{g0}}^{\substack{\text{soil conditioning}\\\text{by grass}}} - \overbrace{\mu_g P_{g0}}^{\text{grass mortality}}\]
\[\frac{dP_{s0}}{dt} = \overbrace{r_sP_{00}(P_{s0} + P_{ss} + P_{sg})}^{\substack{\text{shrub establishment in } \\ \text{empty patch}}} - \overbrace{c_sP_{s0}}^{\substack{\text{soil conditioning}\\\text{by shrub}}} - \overbrace{\mu_sP_{s0}}^{\text{shrub mortality}}\]Patches with plants and corresponding soil conditioning effects
\[\frac{dP_{gg}}{dt} = \overbrace{c_g (P_{g0} + P_{gs})}^{\text{soil conditioning by grass}} + \overbrace{r_g m_{gg} P_{0g}(P_{g0} + P_{gg} + P_{gs})}^{\text{grass establishment in empty grass-conditioned patch}} - \overbrace{\mu_g P_{gg}}^{\text{grass mortality}}\]
\[\frac{dP_{ss}}{dt} = \overbrace{c_s (P_{s0} + P_{sg})}^{\text{soil conditioning by shrub}} + \overbrace{r_s m_{ss} P_{0S}(P_{s0} + P_{ss} + P_{sg})}^{\text{shrub establishment in empty shrub-conditioned patch}} - \overbrace{\mu_s P_{ss}}^{\text{shrub mortality}}\]Patches with no plant present but conditioned soil persists
\[\frac{dP_{0g}}{dt} = \overbrace{\mu_g P_{gg}}^{\text{grass mortality}} + \overbrace{\mu_s P_{sg}}^{\text{shrub mortality}} - \overbrace{r_g m_{gg} P_{0g}(P_{g0}+P_{gg}+P_{gs})}^{\text{grass establishment}} - \overbrace{r_s m_{sg} P_{0g}(P_{s0}+P_{ss}+P_{sg})}^{\text{shrub establishment}}\]
\[\frac{dP_{0s}}{dt} = \overbrace{\mu_s P_{ss}}^{\text{shrub mortality}} + \overbrace{\mu_g P_{gs}}^{\text{grass mortality}} - \overbrace{r_s m_{ss} P_{0s}(P_{s0}+P_{ss}+P_{sg})}^{\text{shrub establishment}} - \overbrace{r_g m_{gs} P_{0s}(P_{s0}+P_{ss}+P_{sg})}^{\text{grass establishment}}\]
Patches with plants growing in the other plant’s conditioned soil
\[\frac{dP_{gs}}{dt} = \overbrace{r_g m_{gs} P_{0s} (P_{g0} + P_{gg} + P_{gs})}^{\text{grass establishment into shrub-conditioned soil}} - \overbrace{\mu_g P_{gs}}^{\text{grass mortality}}\]
\[\frac{dP_{sg}}{dt} = \overbrace{r_s m_{sg} P_{0g} (P_{s0} + P_{ss} + P_{sg})}^{\text{shrub establishment into grass-conditioned soil}} - \overbrace{\mu_s P_{sg}}^{\text{shrub mortality}}\]
Fire disrupts plant–soil feedback
Model predictions
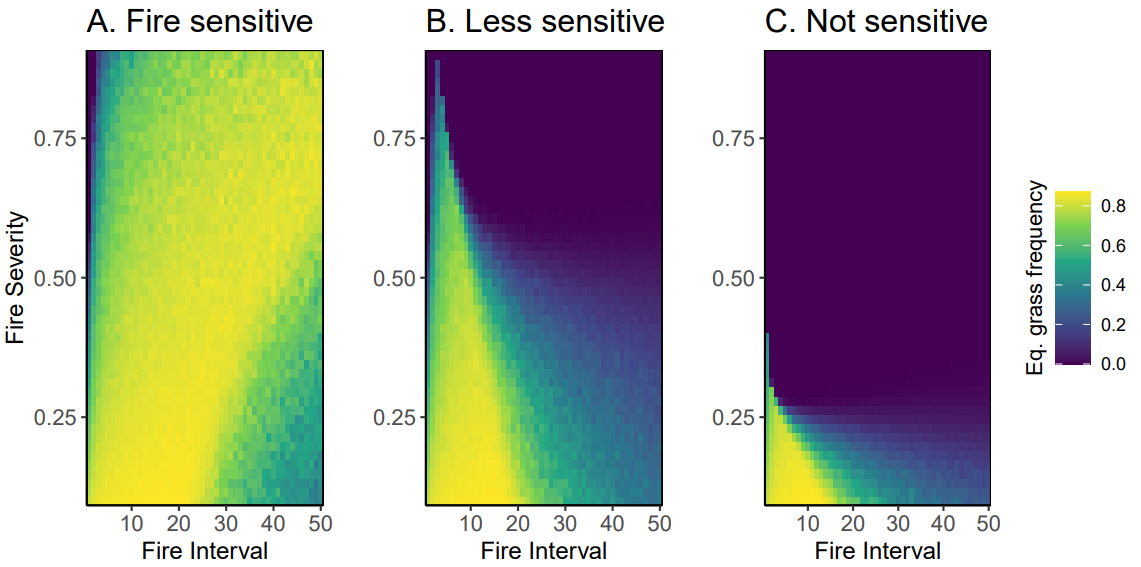
Interpretation: Fire suppression drives microbially driven shrub encroachment – especially if shrubs are insensitive to fire (as they generally are).
Manuscript in prep
Field studies of microbially mediated plant dynamics



Questions:
- How do soil abiotic properties recover post-burn?
- How does fire affect soil microbial composition and function (litter decomposition)?
Plant growth experiment
Question: How do soil communities shape interactions between grasses and shrubs in longleaf pine understories?

Focal species: Big bluestem, Little bluestem, Beaked panicgrass, Beautyberry, Winged sumac, Sweetgum
We are eager to accept any advice on seed germination!
Today’s talk
- Ecological theory for microbial effects on plant coexistence
2. Microbial effects on plant communities in variable environments
Woody encroachment in longleaf pine understories
Coexistence in fragmented tropical forests
Plant eco-evolutionary dynamics under drought
Hassan District, Karnataka, India
Gradients in soil moisture from forest edge to interior
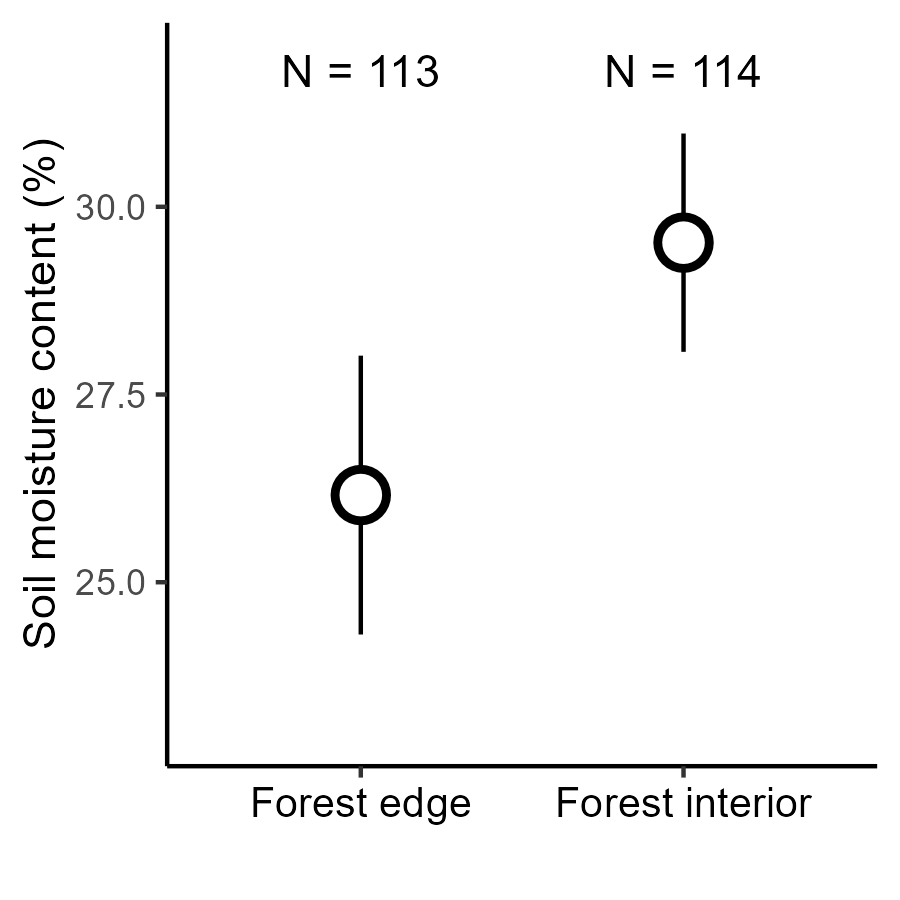
Gradients in soil moisture from forest edge to interior

Gradients in soil moisture from forest edge to interior

Detailed in Krishnadas et al. (2018)
Can variable plant–soil feedback explain this result?
Quantify pairwise plant–soil feedback under high and low water conditions in a shadehouse
Saini, Kandlikar, and Krishnadas in review
Saini, Kandlikar, and Krishnadas in review
Implication: Exaggerated microbially mediated fitness differences in dry soils could contribute to erosion of diversity at fragment edges.
Applications of basic ecology to habitat management

Does a soil-centric perspective help manage coffee invasions and restoration?
Do soil fungi shape tree abundance in tropical forests?
Today’s talk
- Ecological theory for microbial effects on plant coexistence
2. Microbial effects on plant communities in variable environments
Coexistence in fragmented tropical forests
Woody encroachment in longleaf pine understories
Plant eco-evolutionary dynamics under drought
Do microbes regulate plant fitness across generations?
Evidence is accumulating that microbes shape plant stress response
Effects within generations (plasticity) and across generations (e.g. maternal effects, rapid evolution)
Fast-cycling Brassica rapa as a model system for exploring these dynamics


Postbac Scholar
Code
library(tidyverse)
read_csv("brapa-data.csv") |>
select(-x) |>
mutate(Seed = ifelse(Seed == "HW", "High water", "Low water"),
Soil = ifelse(Soil == "HW", "High water", "Low water"),
Current = ifelse(Current == "HW", "High water", "Low water")) |>
pivot_wider(names_from = Type, values_from = y) |>
ggplot(aes(x = Current, y = mean, ymin = sdlo,
ymax = sdhi, fill = Soil, shape = Seed)) +
geom_pointrange(position = position_dodge(width = 0.5),
size = .75) +
scale_shape_manual(values = c(21,23)) +
scale_fill_manual(values = c("#004488", "#bb5566")) +
guides(shape = guide_legend(position = "inside", title =
"Seed history",
override.aes = list(fill = "grey")),
fill = guide_legend(position = "inside",
title = "Soil history",
override.aes = list(shape = 21))) +
ylab("Per-capita fecundity") +
xlab("Contemporary watering") +
labs(caption = "Estimates from a Bayesian GLMM (Poisson family)") +
theme(axis.title = element_text(size = 12),
legend.position = c(0.8, 0.7),
legend.box.background = element_rect(color = "grey", linewidth = 0.5))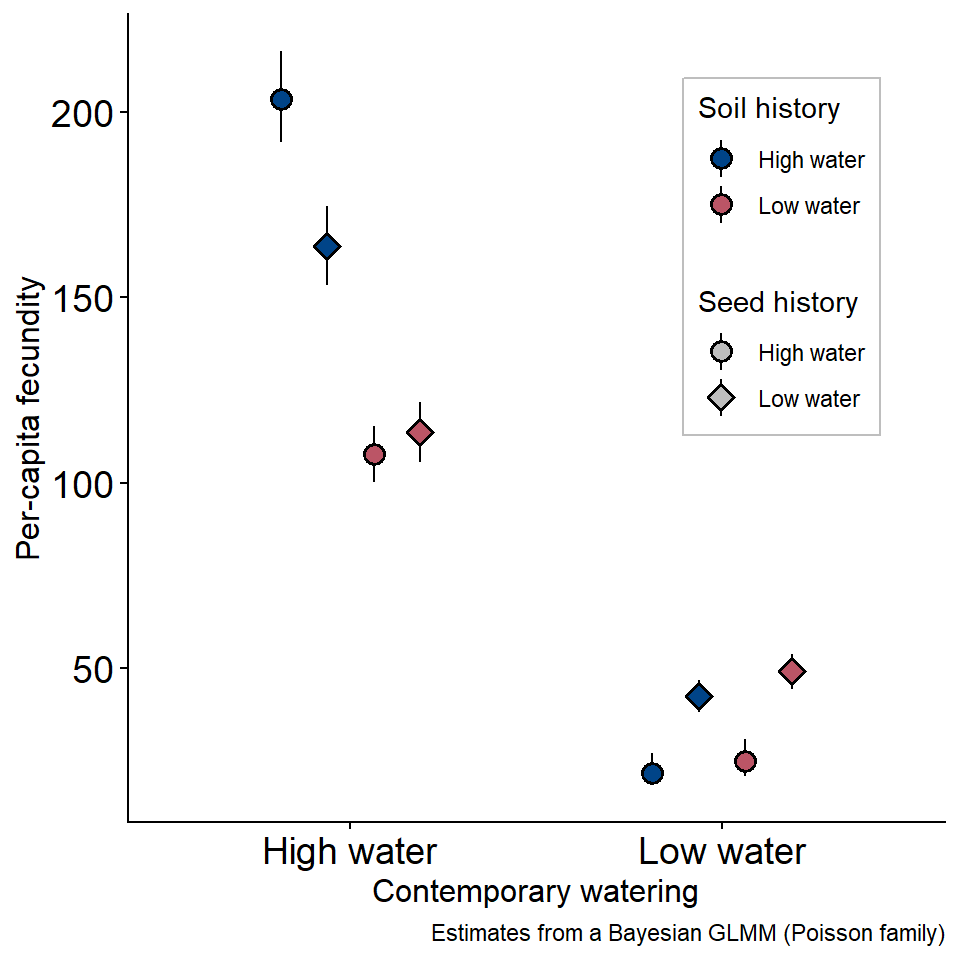
Plant history (maternal effects) and soil history both shape plant response to drought

Other projects in the lab

Plant–mycorrhizal symbiosis under nutrient enrichment

Citizen science for invasion ecology
Other projects in the lab
Fungal drivers of monodominance in tropical forests

Metabolic modeling of symbioses under abiotic stress
Thank you!
slides: https://talks.gklab.org/lsuplantpath-25
contact: gkandlikar@lsu.edu
visit: LSA A363 (\(\Downarrow\))